When Physics Became King – A Book Review (OK, Book Report), part 1

While picking up some books for my dissertation from the science and engineering library, I stumbled across an history book that sounded interesting: When Physics Became King. I enjoy it a lot so far, and hope to remember it, so writing about it seems useful. I also think it brings up some interesting ideas to relate to modern debates, so blogging about the book seems even more useful.

Some recaps and thoughts, roughly in the thematic order the book presents in the first three chapters:

• It’s worth pointing out how deeply tied to politics natural philosophy/physics was as it developed into a scientific discipline in the 17th-19th centuries. We tend to think of “science policy” and the interplay between science and politics as a 20th century innovation, but the establishment of government-run or sponsored scientific societies was a big deal in early modern Europe. During the French Revolution, the Committee of Public Safety suppressed the old Royal Academy and the later establishment of the Institut Nationale was regarded as an important development for the new republic. Similarly, people’s conception of science was considered intrinsically linked to their political and often metaphysical views. (This always amuses me when people hope science communicators like Neil deGrasse Tyson or Bill Nye should shut up, since the idea of science as something that should influence our worldviews is basically as old as modern science.)
• Similarly, science was considered intrinsically linked to commerce, and the desire was for new devices to better reflect the economy of nature by more efficiently converting energy between various forms. I also am greatly inspired by the work of Dr. Chanda Prescod-Weinstein, a theoretical physicist and historian of science and technology on this. One area that Morus doesn’t really get into is that the major impetus for astronomy during this time is improving celestial navigation, so ships can more efficiently move goods and enslaved persons between Europe and its colonies (Prescod-Weinstein discusses this in her introduction to her Decolonizing Science Reading List, which she perennially updates with new sources and links to other similar projects). This practical use of astronomy is lost to most of us in modern society and we now focus on spinoff technology when we want to sell space science to public, but it was very important to establishing astronomy as a science as astrology lost its luster. Dr. Prescod-Weinstein also brings up an interesting theoretical point I didn’t consider in her evaluation of the climate of cosmology, and even specifically references When Physics Became King. She notes that the driving force in institutional support of physics was new methods of generating energy and thus the establishment of energy as a foundational concept in physics (as opposed to Newton’s focus on force) may be influenced by early physics’ interactions with early capitalism.
• The idea of universities as places where new knowledge is created was basically unheard of until late in the 1800s, and they were very reluctant to teach new ideas. In 1811, it was a group of students (including William Babbage and John Herschel) who essentially lead Cambridge to a move from Newtonian formulations of calculus to the French analytic formulation (which gives us the dy/dx notation), and this was considered revolutionary in both an intellectual and political sense. When Carl Gauss provided his thoughts on finding a new professor at the University of Gottingen, he actually suggested that highly regarded researchers and specialists might be inappropriate because he doubted their ability to teach broad audiences.
• The importance of math in university education is interesting to compare to modern views. It wasn’t really assumed that future imperial administrators would use calculus, but that those who could learn it were probably the most fit to do the other intellectual tasks needed.
• In the early 19th century, natural philosophy was the lowest regarded discipline in the philosophy faculties in Germany. It was actually Gauss who helped raise the discipline by stimulating research as a part of the role of the professor. The increasing importance of research also led to a disciplinary split between theoretical and experimental physics, and in the German states, being able to hire theoretical physicists at universities became a mark of distinction.
• Some physicists were allied to Romanticism because the conversion of energy between various mechanical, chemical, thermal, and electrical forms was viewed as showing the unity of nature. Also, empiricism, particularly humans directly observing nature through experiments, was viewed as a means of investigating the mind and broadening experience.
• The emergence of energy as the foundational concept of physics was controversial. One major complaint was that people have a less intuitive conception of energy than forces, which are considered a lot. Others objected that energy isn’t actually a physical property, but a useful calculational tool (and the question of what exactly energy is still pops up in modern philosophy of science, especially in how to best explain it). The development of theories of luminiferous (a)ether are linked a bit to this as an explanation of where electromagnetic energy is – ether theories suggested the ether stored the energy associated with waves and fields.

What is rheology?

Inspired by NaBloPoMo and THE CENTRIFUGE NOT WORKING RIGHT THE FIRST TIME SO I HAVE TO STAY IN LAB FOR THREE MORE HOURS THAN I PLANNED (this was more relevant when I tried writing this a few weeks ago), I’ll be trying to post more often this month. Though heaven knows I’m not even going to pretend I’ll get a post a day when I have a conference (!) to prepare for.

I figure my first post could be a better attempt at better describing a major part of my research now – rheology and rheometers. The somewhat uncommon, unless you’re a doctor or med student who sees it pop up all the time in words like gonorrhea and diarrhea, Greek root “rheo” means “flow”, and so the simplest definition is that rheology is the study of flow. (And I just learned the Greek Titan Rhea’s name may also come from that root, so oh my God, rheology actually does relate to Rhea Perlman.) But what does that really mean? And if you’ve tripped out on fluid mechanics videos or photos before, maybe you’re wondering “what makes rheology different?”

Oh my God, she is relevant to my field of study.

For our purposes, flow can mean any kind of material deformation, and we’re generally working with solids and liquids (or colloid mixtures involving those states, like foams and gels). Or if you want to get really fancy, you can say we’re working with (soft) condensed matter. Why not gas? We’ll get to that later. So what kind of flow behavior is there? There’s viscosity, which is what we commonly consider the “thickness” of a flowing liquid. Viscosity is how a fluid resists motion between component parts to some shearing force, but it doesn’t try to return the fluid back to its original state. You can see this in cases where viscosity dominates over the inertia of something moving in the fluid, such as at 1:00 and 2:15 in this video; the shape of the dye drops is essentially pinned at each point by how much the inner cylinder moves, but you don’t see the fluid move back until the narrator manually reverses the cylinder.

The other part of flow is elasticity. That might sound weird to think of a fluid as being elastic. While you really don’t see elasticity in pure fluids (unless maybe the force is ridiculously fast), you do see it a lot in mixtures. Oobleck, the ever popular mixture of cornstarch and water, becomes elastic as part of its shear-thickening behavior. (Which it turns out we still don’t have a great physical understanding of.)

 

You can think of viscosity as the “liquid-like” part of a substance’s behavior and elasticity as the “solid-like” part. Lots of mixtures (and even some pure substances) show both parts as “viscoelastic” materials. And this helps explain the confusion when you’re younger (or at least younger-me’s questions) of whether things like Jell-O, Oobleck, or raw dough are “really” solid or liquid. The answer is sort of “both”. More specifically, we can look at the “dynamic modulus” G at different rates of force. G has two components – G’ is the “storage modulus” and that’s the elastic/solid part, and G” is the “loss modulus” representing viscosity.

The dynamic moduli of Silly Putty at different rates of stress.

Whichever modulus is higher what mostly describes a material. So in the flow curve above, the Silly Putty is more like a liquid at low rates/frequencies of stress (which is why it spreads out when left on its own), but is more like a solid at high rates (which is why is bounces if you throw it fast enough). What’s really interesting is that the total number of either component doesn’t really matter, it’s just whichever one is higher. So even flimsy shaving cream behaves like a solid (seriously, it can support hair or other light objects without settling) at rest while house paint is a liquid, because even though paint tends to have a higher modulus, the shaving cream still has a higher storage modulus than its own loss modulus.

I want to publish this eventually, so I’ll get to why we do rheology and what makes it distinct in another post.

Quantum Waves are Still Physical, Regardless of Your Thoughts

Adam Frank, founder of NPR’s science and culture blog 13.7, recently published an essay on Aeon about materialism. It’s a bit confusing to get at what he’s trying to say because of the different focus its two titles have, as well as his own arguments. First, the titles. The title I saw first, which is what is displayed when shared on Facebook, is “Materialism alone cannot explain the riddle of consciousness”. But on Aeon, the title is “Minding matter”, with the sub-title or blurb of “The closer your look, the more the materialist position in physics appears to rest on shaky metaphysical ground.” The question of theories of mind is very different than philosophical interpretations of quantum mechanics.

This shows up in the article, where I found it confusing because Franks ties together several different arguments and confuses them with various ideas of “realism” and “materialism”. First, his conception of theories of mind is confusing. I’d say the average modern neuroscientist or other scholar of cognition is a materialist, but I’d be hesitant to say the average one is a reductionist who thinks thought depends very hard on the atoms in your brain. Computational theories of mind tend to be some of the most popular ones, and it’s hard to consider those reductionist. I would concede there may be too much of an experimental focus on reductionism (and that’s what has diffused into pop culture), but the debate over how to move from those experimental techniques to theoretical understanding is occurring: see the recent attempt at using neuroscience statistical techniques to understand Donkey Kong.

I also think he’s making a bit of an odd claim on reductionism in the other sciences in this passage:

A century of agnosticism about the true nature of matter hasn’t found its way deeply enough into other fields, where materialism still appears to be the most sensible way of dealing with the world and, most of all, with the mind. Some neuroscientists think that they’re being precise and grounded by holding tightly to materialist credentials. Molecular biologists, geneticists, and many other types of researchers – as well as the nonscientist public – have been similarly drawn to materialism’s seeming finality.

Yes, he technically calls it materialism, but he seems to basically equate it to reductionism by assuming the other sciences seem fine with being reducible to physics. But, first, Frank should know better from his own colleagues. The solid-state folks in his department work a lot with “emergentism” and point out that the supposedly more reductionist particle people now borrow concepts from them. And he should definitely know from his collaborators at 13.7 that the concept of reducibility is controversial across the sciences. Heck, even physical chemists take issue with being reducible to physics and will point out that QM models can’t fully reproduce aspects of the periodic table. Per the above, it’s worth pointing out that Jerry Fodor, a philosopher of mind and cognitive scientist, who does believe in a computational theory of mind disputes the idea of reductionism. 

This is funny because this tends to be controversial, not because it’s widely accepted.

Frank’s view on the nature of matter is also confusing. Here he seems to be suggesting “materialism” can really only refer to particulate theories of matter, e.g. something an instrument could definitely touch (in theory). But modern fundamental physics does accept fields and waves as real entities. “Shut up and calculate” isn’t useful for ontology or epistemology, but his professor’s pithy response actually isn’t that. Quantum field theories would agree that “an electron is that we attribute the properties of the electron” since electrons (and any particles) can actually take on any value of mass, charge, spin, etc. as virtual particles (which actually do exist, but only temporarily). The conventional values are what one gets in the process of renormalization in the theory. (I might be misstating that here, since I never actually got to doing QFT myself.) I would say this doesn’t mean electrons aren’t “real” or understood, but it would suggest that quantum fields are ontologically more fundamental than the particles are. If it makes more physical sense for an electron to be a probability wave, that’s bully for probability waves, not a lack of understanding. (Also, aside from experiments showing wave-particle duality, we’re now learning that even biochemistry is dependent on the wave nature of matter.)

I’m also not sure the discussion of wave function collapse does much work here. I don’t get why it would inherently undermine materialism, unless a consciousness interpretation were to win out, and as Frank admits, there’s still not much to support one interpretation over the other. (And even then, again, this could still be solved by a materialist view of consciousness.) He’s also ignoring the development of theories of quantum decoherence to explain wavefunction collapse as quantum systems interact with classical environments, and to my understanding, those are relatively agnostic to interpretation. (Although I think there’s an issue with timescales in quantitative descriptions.)

From there, Frank says we should be open to things beyond “materialism” in describing mind. But like my complaint with the title differences, those arguments don’t really follow from the bulk of the article focusing on philosophical issues in quantum mechanics. Also, he seems open to emergentism in the second to last paragraph. Actually, here I think Frank missed out on a great discussion. I think there are some great philosophy of science questions to be had at the level of QFT, especially with regards to epistemology, and especially directed to popular audiences. Even as a physics major, my main understanding of specific aspects of the framework like renormalization are accepted because “the math works”, which is different than other observables we measure. For instance, the anomalous magnetic moment is a very high precision test of quantum electrodynamics, the quantum field theory of electromagnetism, and our calculation is based on renormalization. But the “unreasonable effectiveness of mathematics” can sometimes be wrong and we might lucky in converging to something close. (Though at this point I might be pulling dangerously close to the Duhem-Quine thesis without knowing much of the technical details.) Instead, we got a mediocre crossover between the question of consciousness and interpretations of quantum mechanics, even though Frank tried hard to avoid turning into “woo”.

Why Can’t You Reach the Speed of Light?

A friend from high school had a good question that I wanted to share:

I have a science question!!! Why can’t we travel the speed of light? We know what it is, and that its constant. We’ve even seen footage of it moving along a path (it was a video clip I saw somewhere [Edit to add: there are now two different experiments that have done this. One that requires multiple repeats of the light pulse and a newer technique that can work with just one). So, what is keeping us from moving at that speed? Is it simply an issue of materials not being able to withstand those speeds, or is it that we can’t even propel ourselves or any object fast enough to reach those speeds? And if its the latter, is it an issue of available space/distance required is unattainable, or is it an issue of the payload needed to propel us is simply too high to calculate/unfeasable (is that even a word?) for the project? Does my question even make sense? I got a strange look when I asked someone else…

 This question makes a lot of sense actually, because when we talk about space travel, people often use light-years to discuss vast distances involved and point out how slow our own methods are in comparison. But it actually turns out the road block is fundamental, not just practical. We can’t reach the speed of light, at least in our current understanding of physics, because relativity says this is impossible.

To put it simply, anything with mass can’t reach the speed of light. This is because E=mc² works in both directions. This equation means that the energy of something is its mass times the speed of light squared. In chemistry (or a more advanced physics class), you may have talked about the mass defect of some radioactive compounds. The mass defect is the difference in mass before and after certain nuclear reactions, which was actually converted into energy. (This energy is what is exploited in nuclear power and nuclear weapons. Multiplying by the speed of light square means even a little mass equals a lot of energy. The Little Boy bomb dropped on Hiroshima had 140 pounds of uranium, and no more than two pounds of that are believed to have undergone fission to produce the nearly 16 kiloton blast.)

But it also turns out that as something with mass goes faster, its kinetic energy also turns into extra mass. This “relativistic mass” greatly increases as you approach the speed of light. So the faster something gets, the heavier it becomes and the more energy you need to accelerate it. It’s worth pointing out that the accelerating object hasn’t actually gained material – if your spaceship was initially say 20 moles of unobtanium, it is still 20 moles of material even at 99% the speed of light. Instead, the increase in “mass” is due to the geometry of spacetime as the object moves through it. In fact, this is why some physicists don’t like using the term “relativistic mass” and would prefer to focus on the relativistic descriptions of energy and momentum. What’s also really interesting is that the math underlying this in special relativity also implies that anything that doesn’t have mass HAS to travel at the speed of light.

The kinetic energy of a 1 kg object at various fractions of the speed of light. For reference, 10^18 J is about a tenth of United States’ annual electrical energy consumption.

The graph above represents  the (relativistically corrected) kinetic energy of an 1 kilogram (2.2 pound) object at different speeds. You can basically think of it as representing how much energy you need to impart into the object to reach that speed. In the graph, I started at one ten thousandth the speed of light, which is about twice the speed the New Horizons probe was launched at. I ended it at 99.99% of the speed of light. Just to get to 99.999% of the speed of light would have brought the maximum up another order of magnitude.

Edit to add (9/12/2017): A good video from Fermilab argues against relativistic mass, but concedes it helps introduce relativity to more people.

Quick Thoughts on Diversity in Physics

Earlier this month, during oral arguments for Fisher v. University of Texas, Chief Justice John Roberts asked what perspective an African-American student would offer in physics classrooms. The group Equity and Inclusion in Physics and Astronomy has written an open letter about why this line of questioning may miss the point about diversity in the classroom. But it also seems worth pointing out why culture does matter in physics (and science more broadly).

So nature is nature and people can develop theoretical understanding of it anywhere and it should be similar (I think. This is actually glossing over what I imagine is a deep philosophy of science question.) But nature is also incredibly vast. People approach studies of nature in ways that can reflect their culture. Someone may choose to study a phenomenon because it is one they see often in their lives. Or they may develop an analogy between theory and some aspect of culture that helps them better understand a concept. You can’t wax philosphical about Kekule thinking of ouroboros when he was studying the structure of benzene without admitting that culture has some influence on how people approach science. There are literally entire books and articles about Einstein and Poincare being influenced by sociotechnical issues of late 19th/early 20th century Europe as they developed concepts that would lead to Einstein’s theories of relativity. A physics community that is a monoculture then misses out on other influences and perspectives. So yes, physics should be diverse, and more importantly, physics should be welcoming to all kinds of people.

It’s also worth pointing out this becomes immensely important in engineering and technology, where the problems people choose to study are often immensely influenced by their life experiences. For instance, I have heard people say that India does a great deal of research on speech recognition as a user interface because India still has a large population that cannot read or write, and even then, they may not all use the same language.

The Coolest Part of that Potentially New State of Matter

So we’ve discussed states of matter. And the reason they’re in the news. But the idea that this is a new state of matter isn’t particularly ground-breaking. If we’re counting electron states alone as new states of matter, then those are practically a dime a dozen. Solid-state physicists spend a lot of time creating materials with weird electron behaviors: under this defintion, lots of the newer superconductors are their own states of matter, as are topological insulators.

What is a big deal is the way this behaves as a superconductor. “Typical” superconductors include basically any metal. When you cool them to a few degrees above absolute zero, they lose all electrical resistance and become superconductive. These are described by BCS theory, a key part of which says that at low temperatures, the few remaining atomic vibrations of a metal will actually cause electrons to pair up and all drop to a low energy. In the 1970s, though, people discovered that some metal oxides could also become superconductive, and they did at temperatures above 30 K. Some go as high as 130 K, which, while still cold to us (room temperature is about 300 K), is warm enough to use liquid nitrogen instead of incredibly expensivve liquid helium for cooling. However, BCS theory doesn’t describe superconductivity in these materials, which also means we don’t really have a guide to develop ones with properties we want. The dream of a lot of superconductor researchers is that we could one day make a material that is superconducting at room temperature, and use that to make things like power transmission lines that don’t lose any energy.

This paper focused on an interesting material: a crystal of buckyballs (molcules of 60 carbon atoms arranged like a soccer ball) modified to have some rubidium and cesium atoms. Depending on the concentration of rubidium versus cesium in the crystal, it can behave like a regular metal or the new state of matter they call a “Jahn-Teller metal” because it is conductive but also has a distortion of the soccer ball shape from something called the Jahn-Teller effect. What’s particularly interesting is that these also correspond to different superconductive behaviors. At a concentration where the crystal is a regular metal at room temperatures, it becomes a typical superconductor at low temperatures. If the crystal is a Jahn-Teller metal, it behaves a lot like a high-temperature superconductor, albeit at low temperatures.

This is the first time scientists have ever seen a single material that can behave like both kinds of superconductor. This is exciting becasue this offers a unique testing ground to figure out what drives unconventional superconductors. By changing the composition, researchers change the behavior of electrons in the material, and can study their behavior, and see what makes them go through the phase transition to a superconductor.

What is a State of Matter?

This Vice article excitedly talking about the discovery of a new state of matter has been making the rounds a lot lately. (Or maybe it’s because I just started following Motherboard on Twitter after a friend pointed this article out) Which lead to two good questions: What is a state of matter? And how do we know we’ve found a new one? We’ll consider that second one another time.

In elementary school, we all learned that solid, liquid, and gas were different states of matter (and maybe if you’re science class was ahead of the curve, you talked about plasma). And recent scientific research has focused a lot on two other states of matter: the exotic Bose-Einstein condensate, which is looked at for many experiments to slow down light, and the quark-gluon plasma, which closely resembles the first few milliseconds of the universe after the Big Bang. What makes all of these different things states? Essentially a state of matter is the set behavior of the collection of particles that makes up your object of interest, and each state behaves so differently you can’t apply the description one to another. A crucial point here is that we can only consider multiple partcies to be states, and typically a large number of particles. If you somehow have only one molecule of water, it doesn’t really work to say whether it is solid, liquid, or gas because there’s no other water for it to interact with to develop collective properties.

So room temperature gold and ice are solids because they’re described by regular crystal lattices that repeat. Molten gold and water are no longer solids because they’re no longer described by a regular crystal structure but still have relatively strong forces between molecules. The key property of a Bose-Einstein condensate is that most of its constituent particles are in the lowest possible energy. You can tell when you switched states (a phase transition) because there was a discontinuous change in energy or a property related to energy. In everyday life, this shows up as the latent heat of melting and the latent heat of vaporization (or evaporation).

The latent heat of melting is what makes ice so good at keeping drinks cold. It’s not just the fact that ice is colder than the liquid; the discontinuous “jump” of energy required to actually melt 32°F  ice into 32°F water also absorbs a lot of heat. You can see this jump in the heating curve below. You also see this when you boil water. Just heating water to 212 degrees Fahrenheit doesn’t cause it all to boil away; your kettle/stove also has to provide enough heat to overcome the heat of vaporization. And that heating is discontinuous because it doesn’t raise the temperature until the phase transition is complete. You can try this for yourself in the kitchen with a candy thermometer: ice will always measure 32 F, even if  you threw it in the oven, and boiling water will always measure 212 F.

The heating curve of water. The horizontal axis represents how much heat has been added to a sample of water. The vertical axis shows the temperature. The flat lines are where heat is going into the latent heat of the phase transition instead of raising the temperature of the sample.

There’s also something neat about another common material related to phase transitions. The transition between a liquid and a glass state does not have a latent heat. This is the one thing that makes me really sympathetic to the “glasses are just supercooled liquids” views. Interestingly, this also means that there’s really no such thing as a single melting temperature for a given glass, because the heating/cooling rate becomes very important.

But then the latter bit of the article confused me, because to me it points out that “state of matter” seems kind of arbitrary compared to “phase”, which we talk about all the time in materials science (and as you can see, we say both go through “phase” transitions). A phase is some object with consistent properties throughout it, and a material with the same composition can be in different phases but still in the same state. For instance, there actually is a phase of ice called ice IX, and the arrangement of the water molecules in it is different from that in conventional ice, but we would definitely still consider both to be solids. Switching between these phases, even though they’re in the same state, also requires some kind of energy change.

Or if you heat a permanent magnet above its critical temperature and caused it to lose its magnetization, that’s the second kind of phase transition. That is, while the heat and magnetization may have changed continuously, the ease of magnetizing it (which is the second derivative of the energy with respect to strength of the magnetic field) had a jump at that point. Your material is still in a solid state and the atoms are still in the same positions, but it changed its magnetic state from permanent to paramagnetic. So part of me is wondering whether we can consider that underlying electron behavior to be a definition of a state of matter or a phase. The article makes it sound we’re fine saying they’re basically the same thing. This Wikipedia description of “fermionic condensates” as a means to describe superconductivity also supports this idea.

Going by this description then means we’re surrounded by way more states of matter than the usual four we consider. With solids alone, you interact with magnetic metals, conductors (metals or the semiconductors in your electronics), insulating solids, insulating glasses, and magnetic glasses (amorphous metals are used in most of those theft-prevention tags you see) on a regular basis, which all have different electron behaviors. It might seem slightly unsatisfying for something that sounds as fundamental as “states of matter” to end up having so many different categories, but it just reflects an increasing understanding of the natural world.

Carbon is Dead. Long Live Carbon?

Last month, the National Nanotechnology Initiative released a report on the state of commercial development of carbon nanotubes. And that state is mostly negative. (Which pains me, because I still love them.) If you’re not familiar with carbon nanotubes, you might know of their close relative, graphene, which has been in the news much more since the Nobel Prize awarded in 2010 for its discovery. Graphene is essentially a single layer of the carbon atoms found in graphite. A carbon nanotube can be thought of as rolling up a sheet of graphene into a cylinder.

Visualizing a single-walled (SW) carbon nanotube (CNT) as the result of rolling up a sheet of graphene.

If you want to use carbon nanotubes, there are a lot of properties you need to consider. Nearly 25 years after their discovery, we’re still working on controlling a lot of these properties, which are closely tied to how we make the nanobues.

Carbon nanotubes have six major characteristics to consider when you want to use them:

• How many “walls” does a nanotube have? We often talk about the single-walled nanotubes you see in the picture above, because their properties are the most impressive. However, it is much easier to make large quantities of nanotubes with multiple walls than single walls.
• Size. For nanotubes, several things come in play here.
  • The diameter of the nanotubes is often related to chirality, another important aspect of nanotubes, and can affect both mechanical and electrical properties.
  • The length is also very important, especially if you want to incorporate the nanotubes into other materials or if you want to directly use nanotubes as a structural material themselves. For instance, if you want to add nanotubes to another material to make it more conductive, you want them to be long enough to routinely touch each other and carry charge through the entire material. Or if you want that oft-discussed nanotube space elevator, you need really long nanotubes, because stringing a bunch of short nanotubes together results in a weak material.
  • And the aspect ratio of length to width is important for materials when you use them in structures.
• Chirality, which can basically be thought of as the curviness of how you roll up the graphene to get a nanotube (see the image below). If you think of rolling up a sheet of paper, you can roll it leaving the ends matched up, or you can roll it an angle. Chirality is incredibly important in determing the way electricity behaves in nanotubes, and whether a nanotube behaves like a metal or like a semiconductor (like the silicon in your computer chips). It also turns out that the chirality of nanotubes is related to how they grow when you make them.
• Defects. Any material is always going to have some deviation from an “ideal” structure. In the case of the carbon nanotubes, it can be missing or have extra carbon atoms that replace a few of the hexagons of the structure with pentagons or heptagons. Or impurity atoms like oxygen may end up incorporated into the nanotube. Defects aren’t necessarily bad for all applications. For instance if you want to stick a nanotube in a plastic, defects can actually help it incorporate better. But electronics typically need nanotubes of the highest purity.

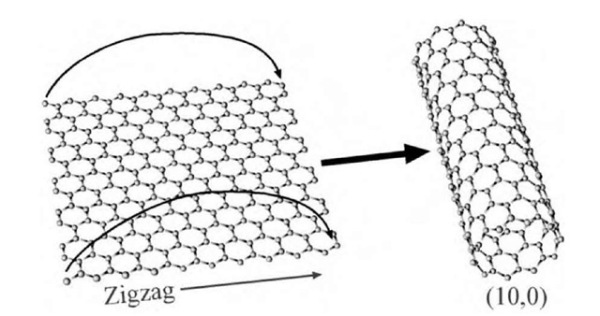
Some of the different ways a nanotube can be rolled up. The numbers in parentheses are the “chiral vector” of the nanotube and determine its diameter and electronic properties.

Currently, the methods we have to make large amounts of CNTs result in a mix of ones with different chiralities, if not also different sizes. (We have gotten much better at controlling diameter over the last several years.) For mechanical applications, the former isn’t much of a problem. But if you have a bunch of CNTs of different conductivities, it’s hard to use them consistently for electronics.

But maybe carbon nanotubes were always doomed once we discovered graphene. Working from the idea of a CNT as a rolled-up graphene sheet, you may realize that means there are  way more factors that can be varied in a CNT than a single flat flake of graphene. When working with graphene, there are just three main factors to consider:

• Number of layers. This is similar to the number of walls of a nanotube. Scientists and engineers are generally most excited about single-layer graphene (which is technically the “true” graphene). The electronic properties change dramatically with the number of layers, and somewhere between 10 and 100 layers, you’re not that different from graphite. Again, the methods that produce the most graphene produce multi-layer graphene. But all the graphene made in a single batch will generally have consistent electronic properties.
• Size. This is typically just one parameter, since most methods to make graphene result in roughly circular, square, or other equally shaped patches. Also, graphene’s properties are less affected by size than CNTs.
• Defects. This tends to be pretty similar to what we see in CNTs, though in graphene there’s a major question of whether you can use an oxidized form or need the pure graphene for your application, because many production methods make the former first.

Single-layer graphene also has the added quirk of its electrical properties being greatly affected by whatever lies beneath it. However, that may be less of an issue for commercial applications, since whatever substrate is chosen for a given application will consistently affect all graphene on it. In a world where can now make graphene in blenders or just fire up any carbon source ranging from Girl Scout cookies to dead bugs and let it deposit on a metal surface, it can be hard for nanotubes to sustain their appeal when growing them requires additional steps of catalyst production and placement.

But perhaps we’re just leaving a devil we know for a more hyped devil we don’t. Near the end of last year, The New Yorker had a great article on the promises we’re making for graphene, the ones we made for nanotubes, and about technical change in general, which points out that we’re still years away from widespread adoption of either material for any purpose. In the meantime, we’re probably going to keep discovering other interesting nanomaterials, and just like people couldn’t believe we got graphene from sticky tape, we’ll probably be surprised by whatever comes next.

A Nobel for Nanotubes?

A popular pastime on the science blogosphere is doing Nobel predictions; educated guesses on who you think may win a Nobel prize in the various science categories (physics, chemistry, and physiology or medicine). I don’t feel like I know enough to really do detailed predictions, but I did make one. Okay, more of a dream than a prediction. But I feel justified because Slate also seemed to vouch for it. What was it? I think a Nobel Prize in Physics should be awarded for the discovery and study of carbon nanotubes.

One potential issue with awarding a prize for carbon nanotube work could be priority. Nobel prizes can only be split between three people. While Iijima is generally recognized as the first to discover carbon nanotubes, it actually seems that they have really been discovered multiple times (in fact, Iijima appears to have imaged a carbon nanotube in his thesis nearly 15 years before what is typically considered his “discovery”). It’s just that Iijima’s announcement happened to be at a time and place where the concept of a nanometer-sized cylinder of carbon atoms could both be well understood and greatly appreciated as a major focus of study. The paper linked to points out that many of the earlier studies that probably found nanotubes were mainly motivated by PREVENTING  their growth because they were linked to defects and failures in other processes. The committee could limit this by awarding the prize for the discovery of single-walled nanotubes, which brings the field of potential awardees down to Iijima and one of his colleagues and a competing group at IBM in California. This would also work because a great deal of the hype of carbon nanotubes is focused on single-walled tubes because they generally have superior properties than their multi-walled siblings and theory focuses on them.

No matter what, I would say Mildred Dresselhaus should be included in any potential nanotube prize because she has been one of the most important contributors to the theoretical understanding of carbon nanotubes since the beginning. She’s also done a lot of theoretical work on graphene, but the prize for graphene was more experimental because while theorists have been describing graphene since at least the 80s (Dresselhaus even has a special section in that same issue), no one had anything pure to work with until Geim and Novoselov started their experiments.

In 1996, another form of carbon was also recognized with the Nobel Prize in Chemistry. Rick Smalley, Robert Curl, and Harold Kroto won the prize for their discovery of buckminsterfullerene (or “buckyballs”) in 1985 and further work they did with other fullerenes and being able to the prove these did have ball-like structures. So while the prize for graphene recognized unique experimental work that could finally test theory, this prize was for an experimental result no one was expecting.   Pure carbon has been known to exist as a pure element in two forms, diamond and graphite, for a long time and no one was expecting to find another stable form. Fullerenes opened people’s minds to nanostructures and served as a practical base for the start of much nanotechnology research, which was very much in vogue after Drexler’s discussions in the 80s.

Six phases of carbon. Graphite and diamond are the two common phases we encounter in normal conditions.

So why do I think nanotubes should get the prize? One could argue it just seems transitional between buckyballs and graphene, so it would be redundant. While a lot of work using nano-enhanced materials does now focus on graphene, a great deal of this is based on previous experiments using carbon nanotubes, so the transition was scientifically important. And nanotubes still have some unique properties. The shape of a nanotube immediately brings lot of interesting applications to mind that wouldn’t come up for flat graphene or the spherical buckyballs: nano-wires, nano “test tubes”, nano pipes, nanomotors, nano-scaffolds, and more.  (Also, when describing nanotubes, it’s incredibly easy to be able to say it’s like nanometer-sized carbon fiber, but I realize that ease of generating one sentence descriptions is typically not a criterion for Nobel consideration.) The combination of these factors make nanotubes incredibly important in the history of nanotechnology and helped it transition into the critical field it is today.

What Happens When You Literally Hang Something Out to Dry?

I got a question today!  A good friend from high school asked:

Hey! So I have a sciencey question for you. But don’t laugh at me! It might seem kinda silly at first, but bear with me. Ok, how does water evaporate without heat? Like a towel is wet, so we put it in the sun to dry (tada heat!) but if its a kitchen or a bathroom towel that doesn’t see any particular increase in temp? How does the towel dry? What happens to the water? Does it evaporate but in a more mild version of the cycle of thinking?

It’s actually a really good question, and the answer depends on some statistical physics and thermodynamics. You know water is turning into water vapor all the time around you, but you can also see that these things clearly aren’t boiling away.

I’ve said before that temperature and heat are kind of weird, even though we talk about them all the time:

It’s not the same thing as energy, but it is related to that.  And in scientific contexts, temperature is not the same as heat.  Heat is defined as the transfer of energy between bodies by some thermal process, like radiation (basically how old light bulbs work), conduction (touching), or convection (heat transfer by a fluid moving, like the way you might see soup churn on a stove).  So as a kind of approximate definition, we can think of temperature as a measure of how much energy something could give away as heat.

The other key point is that temperature is only an average measure of energy, as the molecules are all moving at different speeds (we touched on this at the end of this post on “negative temperature”). This turns out to be crucial, because this helps explain the distinction between boiling and evaporating a liquid. Boiling is when you heat a liquid to its boiling point, at which point it overcomes the attractive forces holding the molecules together in a liquid. In evaporation, it’s only the random molecules that happen to be moving fast enough to overcome those forces that leave.

We can better represent this with a graph showing the probabilities of each molecule having a particular velocity or energy. (Here we’re using the Maxwell-Boltzmann distribution, which is technically meant for ideal gases, but works as a rough approximation for liquids.) That bar on the right marks out an energy of interest, so here we’ll say it’s the energy needed for a molecule to escape the liquid (vaporization energy). At every temperature, there will always be some molecules that happen to have enough energy to leave the liquid. Because the more energetic molecules  leave first, this is also why evaporating liquids cool things off.

Maxwell-Boltzmann distributions of the energy of molecules in a gas at various temperatures. From http://ibchem.com/IB/ibnotes/full/sta_htm/Maxwell_Boltzmann.htm

You might wonder that if say, your glass of water or a drenched towel is technically cooling off from evaporation, why will it completely evaporate over time? Because the water will keep warming up to room temperature and atomic collisions will keep bringing up the remaining molecules back to a similar Boltzmann distribution.

My friend also picks up on a good observation comparing putting the towel out in the sun versus hanging it in a bathroom. Infrared light from the sun will heat up the towel compared to one hanging around in your house, and you can see that at the hotter temperatures, more molecules exceed the vaporization energy, so evaporation will be faster. (In cooking, this is also why you raise the heat but don’t need to boil a liquid to make a reduction.)

There’s another factor that’s really important in evaporation compared to boiling. You can only have so much water in a region of air before it starts condensing back into a liquid (when you see dew or fog, there’s basically so much water vapor it starts re-accumulating into drops faster than they can evaporate). So if it’s really humid, this process goes slower. This is also why people can get so hot in a sauna. Because the air is almost completely steam, their sweat can’t evaporate to cool them off.